|
- United States Patent 3,623,156
Assigned to Hewlett-Packard, inventor Thomas E. Osborne.
Filed May 26, 1969 and granted November 23, 1971.
The patent has a total of 61 pages, including corrections, that
describe the calculator's various modules and sequencing.
- Hewlett-Packard Journal, September 1968
|
Has four articles describing various aspects of the machine:
- "A New Electronic Calculator with Computer-like Capabilities"
- "Hardware Design of the Model 9100A Calculator"
- "Internal Programming of the 9100A Calculator"
- "How the Model 9100A Was Developed"
|
|
 |
- Hewlett-Packard Journal, October 1970
"More Memory for Desktop Calculators"
- Hewlett-Packard KEYBOARD, Winter 1970
|
From the inside front cover:
TO HEWLETT-PACKARD CALCULATOR USERS
The HP KEYBOARD is published quarterly to
make the latest programs and application ideas available
to all HP 9100 calculator owners.
Your programs, both of general interest and in specialized applications
categories, will help to keep other calculator owners better informed
and increase the efficiency with which the HP 9100 is utilized
throughout the world. Please send your programs to the
HP KEYBOARD editor.
|
|
- Inventions of Opportunities: Matching Technology with Market Needs ,
Selections from the pages of the Hewlett-Packard Journal
(c) 1983 by Hewlett-Packard Company
ISBN 0-9612030-0-5
Pages 127 through 144 reproduce five articles from Volume 20,
Number 1 (September 1968) of the Hewlett-Packard Journal.
This book also has three articles from Volume 23, Number 10 (June 1972)
regarding the HP-35 and four articles from Volume 25, Number 9 (May 1974)
covering the HP-65. It also has two articles on the HP-IB (now IEEE 488)
interface bus from Volume 24, Number 2 (October 1972).
-
How It All Began: Hewlett-Packard's Loveland Facility ,
Kenneth Jensen
(c) 1999 by Agilent Technologies
ISBN 1-928656-02-1
From page 71 and continuing:
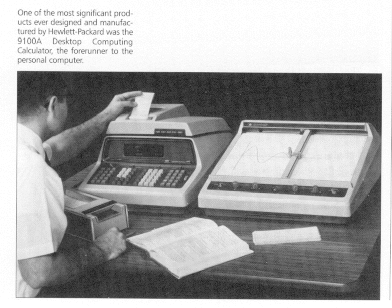
One of the most significant products ever designed and manufactured by
Hewlett-Packard was introduced in March 1968. This was the 9100A
Desktop Computing Calculator, the forerunner to the personal computer
or PC. The 9100A was the first, totally self-contained programmable unit
of its kind which could fit on a desk. It included a display with
three registers and a magnetic card reader. An optional printer, which
fit neatly on the top of the 9100A, was offered separately. The 9100A
used a ten-layer, PC board ROM for its algorithms, including log and
trig functions. Its volatile core memory used small ferrite rings through
which were woven copper wires. The initial price of $4900 was rather
steep, and it was later lowered to $4,400. The 9100A was about the size
and weight of an IBM typewriter. This product represented a significant
departure for the Loveland Division's existing line of measurement
equipment.
The 9100A's performance seems insignificant today with limited internal
memory that stored only 196 steps. It was truly innovative for its
time, however. The 9100A spawned an entire line of desktop calculators
developed by the Calculator Products Division at Loveland under the
direction of Tom Kelley. The Fort Collins Division was formed to carry
on this product line.
Development of the 9100A started in 1965 in Palo Alto when a physicist
named McMillian approached HP with a small calculator he invented.
Tom Osborne, another inventor, also approached HP with his own home-built
calculator. The best features of the two products were combined, and
Osborne was hired as a consultant to continue the development work in
HP Labs. The original size of the product was reduced by the invention
of a PC board ROM by Chuck Near. Once the product's design was found
feasible, it was transferred to to the Loveland Division. Chuck Near
came along with the product.
Responding to the wish of Arthur C. Clarke, author of
2001: A Space Odyssey, he was presented a 9100A in April, 1970.
The unit was given to Clarke by Barney Oliver, Director of HP Labs.
- Computer Structures: Readings and Examples ,
G. Gordon Bell and Allen Newell
(c) 1971 by McGraw-Hill, Inc.
ISBN 07-004357-4
Chapter 20, pages 243 to 256, is entitled The HP Model 9100A
computing calculator, which is a compilation of three
articles from the September 1968 issue of the Hewlett-Packard
Journal.
Good photographs and diagrams.
You can view this chapter on-line
here, although the pictures aren't so great.
- Electronics World, September 1971
An engineer by the name of Paul Asmus, from HP's Calculator
Products Division, wrote an article espousing the virtues
of the programmable calculator. Although not mentioned by
name in the text, the 9100 does make several appearances
in photos that accompany the article.
I've scanned the article and converted it to HTML. You
can read the entire article and see the photos by clicking
here.
- Introduction to Computers and Computer Science,
Richard C. Dorf
(c) 1972 by Boyd and Frasier Publishing Company
ISBN 0-87835-025-X
Pages 103 through 122 cover the 9100 in some detail, describing
the representation schemes for fixed and floating point numbers
and moving into programming concepts and instructions.
(Note that the second edition does not have this section. It
was replaced by a more generic discussion of programmable
calculators, along with a picture of a Wang calculator and a
caption describing the HP 9825A.)
- Proceedings of the IEEE, March 1984
This "special issue" devoted to personal computers contains an
article entitled The Design and Development of a Family
of Personal Computers for Engineers and Scientists authored
by Gerald Nelson and William Hewlett.
The article describes the 9100A and 9100B in a few paragraphs, and
goes on to posit:
Our intent for the 9100 products was very clear in our minds.
We were a team of scientists and engineers who wanted to build
personal computers for other scientists and engineers. In
retrospect, it is interesting to consider to what degree the 9100A
should be considered the first mass-produced personal computer.
A technology assessment of personal computers was conducted for the
National Science Foundation by a research team at the University of
Southern California, Los Angeles. The report, issued in September
of 1980, acknowledges that it is difficult exactly to define
"personal computer," but gives definitions containing the following
criteria:
- small, stand-alone
- general purpose
- advanced microelectronics technology (microprocessor)
- operated by a single individual, interactively
- no requisite computer training
- affordable by an individual or small group
The report concludes: "the distinction of being the first mass-produced
personal computer (PC) probably belongs to the ALTAIR 8800 marketed in
late 1974 by the small Albuquerque-based firm, MITS, Inc." (The Altair
8800 was based on the Intel 8080 microprocessor which was first delivered
in 1973.) The HP 9100 machines substantially satisfied the above
criteria. Microprocessors, of course, were not used in the 9100 since
they did not then exist. Those who would argue that the 9100 was too
specialized to be considered the first personal computer would almost
certainly agree that the distinction is merited by one of the
subsequent 9800 Series computers that provided full algebraic language
capability and still predated 1974.
(The report to which the article refers is
"Technical Assessment of Personal Computers," vols I, II,
University of Southern California, Los Angeles,
U.S. Department of Commerce NTIS, September 1980.)
- The ANALYTICAL ENGINE, May 1995
Volume 2, number 3 of the
Journal of the Computer History Association of California
(ISSN 1071-6351) has an interview beginning on page 8 with the late
Dr. Bernard Oliver regarding, in part, the development of the HP 9100.
The issue can be read
here.
A local copy is
here.
| |
In 1968 Hewlett-Packard introduced the 9100A calculator,
a programmable reverse-polish notation (RPN) computing machine
that could rapidly perform floating point, trigonometric and
hyperbolic functions as well as vector and polar operations.
It came with a built-in magnetic card reader/writer for program and
data storage. It used a CRT (cathode ray tube) for display
of three data registers.
