THE PROBLEM   Before you can do anything with a communications satellite you have to know where it is at every instant of its motion around the earth. In other words, you need to know its orbit quite accurately. When you know this, you can predict when a particular station on the ground will be able to see the satellite and communicate with it. You also can tell when two or more stations can see the satellite simultaneously and communicate with each other. And you can estimate how many satellites will be needed to provide a group of ground stations with enough working time to maintain a communications service. This last, after all, is the ultimate goal of all our efforts in the communications satellite field.

In determining a satellite's orbit, we find that we must do three things:

• We must obtain information on the position - and perhaps also the velocity - of the satellite whenever possible by observing it with scientific instruments.
• We must use this information to determine the satellite's orbit at the time of the observations.
• We must be able to tell how this orbit changes between the times when we observe it, because a satellite's orbit does not remain constant with the passage of time.

In the case of the Echo I satellite, we engaged in the first and third of these activities. We had many changes to follow the satellite with our radars, and we could speculate how its orbit was changing through the months. In the case of the Telstar I satellite, we engaged in all three kinds of activity. We shall take a look at these problems in the sequence in which we came across them for both the Echo and Telstar satellites.

How We Track Satellites

We collect on the ground most of the information to calculate a satellite's orbit, using optical instruments or radar equipment. Following a satellite through the sky is called tracking; in the early days after the first Sputniks, some of this tracking was done with the naked eye or with very simple telescopes by the Moonwatch teams. Many of you may have observed Echo I on a clear night without any kind of instrument.

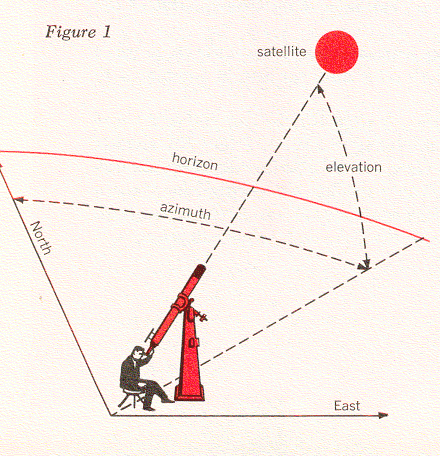
If we use a telescope, we note the time of the observation and we usually take a photograph of the satellite. We locate the satellite in terms of the two angles shown in Figure 1. One of these is the elevation angle - the number of degrees a telescope must be tilted above the horizon to see the satellite. The second is the azimuth angle - the number of degrees between the plane in which we measure the elevation angle and the north direction. Of course, we can also point a radar antenna at the satellite in the same manner. The radar can receive a signal transmitted by the satellite, or else it can send a signal to the satellite and watch for the reflected waves that eventually return. In the latter case, the satellite must have sufficient surface area to produce an adequate reflected signal. These two kinds of precision tracking were both possible with Echo I. Radar can also do something that optical equipment usually can't do: measure the distance out to the satellite.

The Basic Physics of Satellite Motion

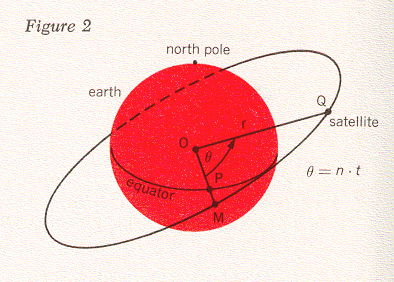
The Echo I satellite was launched into a circular orbit inclined at an angle to the place of the earth's equator. In Figure 2, this equatorial plane intersects the plane of the satellite orbit along the line OPM. The point O represents the center of the earth, the point M is on the satellite orbit, and the point P is on the equator. At any instant, the satellite may be located in its orbit by the angle θ, which is measured between the line OM and the line OQ, where the point Q is the satellite's location. If the satellite moves in a circular orbit, as in this case, the angle θ is proportional to time. That is, we can write θ = nt. We call n the angular speed of the satellite; one way of measuring this is in degrees per second.

Thus, the satellite is whirling at a constant speed about the earth like a stone tied to a string. Let us examine the physics of this situation a little more closely with the help of Figure 3. If the satellite is moving with the velocity v, then we know that the centrifugal force acting on it is

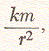
where m is the mass of the satellite and r is its distance from the center of the earth. Obviously, no string ties the satellite to the earth, but the force of gravitational attraction between the earth and the satellite has the same effect. Newton's law of mutual attraction tells us that this force is proportional to the product of the two masses divided by the square of the distance between their centers, or

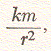
where k is a constant that essentially represents the mass of the earth [This is obtained from k = gR², where g is the acceleration due to gravity and R is the radius of the earth. (Here, we can use k = 96,500 miles³ per second².]. Newton's law also tells us that this force will be pointing toward the center of the earth if the earth is spherical. When the satellite is in circular motion, the centrifugal force and the gravitational force must balance each other. Hence we have

and from this we can solve to find that the velocity of the satellite must be equal to

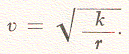
In the case of the Echo I satellite, which was designed to have a radial distance of r = 5000 miles, this velocity amounts to about 4.4 miles per second. The time for one revolution in orbit is obtained with the formula

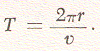
For the Echo satellite this time, T, turns out to be just about two hours.

Calculating the Orbit of Echo I

These basic phyiscal principles of satellite motion can give us many useful answers. They tell us how fast we must move a precision tracker to follow the satellite through the sky, how much time a satellite will spend above the horizon, and how long will be the time from one chance of seeing it to the next. However, in the Echo project we were not merely concerned with planning our experiments from hour to hour; we also needed to know how the satellite would move for weeks and perhaps months in advance. When you study the motion of a satellite over such a length of time, you discover that its circular orbit will not remain the same as it was at launch. This fact had been observed on other satellites and was to be expectedc also with Echo.

In everything we have said so far it was assumed that the earth was a perfect sphere, which is the way a geographer's globe presents it to us. In reality, the earth is somewhat flattened, with its diameter from the north pole to the south pole being somewhat shorter than its diameter at the equator. One way of looking at this is to visualize the earth as a sphere with some material added in the equatorial zone, which we may call equatorial bulge. This bulge causes Echo's orbit to have a slow "wobble" about the earth's polar axis, somewhat like that of a spinning top.

Another force that makes the satellite's orbit shift slightly is the faint pressure caused by the light from the sun. Although this pressure is much too small for us to perceive without the help of very delicate instruments, it is enough to affect a satellite, which has nothing to support it in space and is exposed to solar pressure for a very long time. Since the Echo balloon is a plastic sphere, 100 feet in diameter, that weighs only a little more than 100 pounds, the light rays striking its surface are enough to cause a second "wobble" effect. This wobble centers about the line from the earth to the sun. Light pressure also forces the orbit to go slightly out of round from a perfect circle, and other gradual effects on the satellite's orbit are caused by the gravitational attraction of the moon and the sun.

All these disturbances are ever-present and act simultaneously, and a satellite's total response to them is very complicated. Fortunately, however, most of the changes take place at a very slow and uniform rate, and we can predict them fairly accurately.

Calculating the Orbit of Telstar I

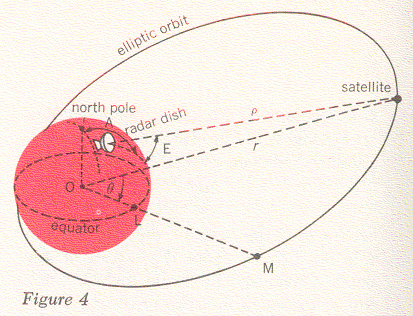
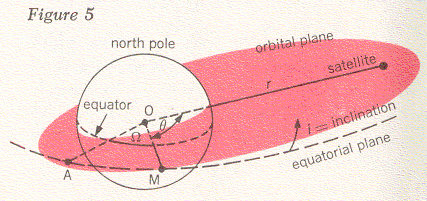
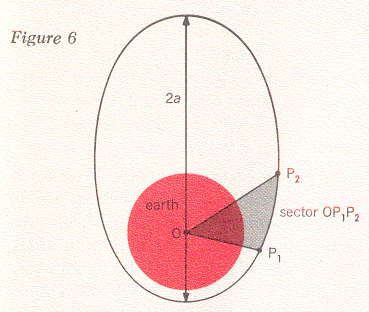
In Project Telstar we had to calculate the satellite's orbit from observations made by our precision trackers. This introduced a few problems in addition to the ones we encountered with Project Echo. In the first place, the orbit of the Telstar satellite is an elongated ellipse, as indicated in Figure 4, rather than being almost circular, as in the case of Echo I. We mentioned earlier that a precision tracker can furnish data on a satellite's elevation angle, E, and azimuth, A (see Figure 1). It can also give us a reading for ρ, the distance from the tracker to the satellite (Figure 4). If we know the position of the tracker on the earth, we can reduce the quantities A, E, and ρ to the angle θ and the distance r (measured from the center of the earth to the satellite). These two quantities locate the satellite in the plane of its orbit, but in order to describe its position completely we must also specify this orbital plane. In Figure 5 the orbital plane is shown as a shaded surface, with θ and r being the same as before. You will recall that the line OM represents the intersection between this plane and the equatorial plane; we call the angle i between the two planes the inclination of the orbit. Finally, we have the angle Ω between the line OM and some line OA to the point A, which we can choose as any convenient spot in the equatorial plane. Now we have specified the orbital plane completely. The point A can be found from day to day by fixing its position relative to a certain star in the sky.

Figures 4 and 5 tell us something about the geometry of the satellite's position in space, but for the complete story we must also give the time at which it can be found there. For this purpose, there are some astronomical laws that relate position on an elliptic orbit to time. Two of these are illustrated in Figure 6; in looking at this figure, you should imagine that you are standing off to one side of the orbital plane to get a good view of the entire orbit. The longest dimension of the ellipse, 2a, is called the major axis; this dimension is related to the satellite's period - the time it takes to go once around the ellipse. More than three hundred years ago the astronomer Johannes Kepler observed that the period T, of an ellipse is

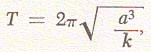
where k again was (using Newton's work) essentially the mass of the earth.

Instead of a complete revolution, we may only be concerned with part of one orbit. Let's say that this part lies between the two positions P₁ and P₂ that the satellite occupies at the two times t₁ and t₂ (see Figure 6). Then another of Kepler's laws says that the ratio between the time difference t₂ - t₁ and the period T equals the ratio between the sector of the ellipse OP₁P₂ and the area of the entire ellipse.

Now let us see how we can use the quantities r, θ, i, and Ω as well as Kepler's two time laws to determine the motion of the satellite in space. Suppose that we have made observations of the Telstar at two times t₁ and t₂ and that we have measured its distance along lines ρ₁ and ρ₂ in Figure 7. In other words, we know that at these two times the satellite was at the points P₁ and P₂. Since three points determine a plane, we know in this case that P₁, P₂, and O define the satellite orbital plane. Knowing this, we can now calculate the angles θ₁ and θ₂, the distances r₁ and r₂, and the angles i and Ω. (The detailed formulas for this are derived from analytic geometry.)

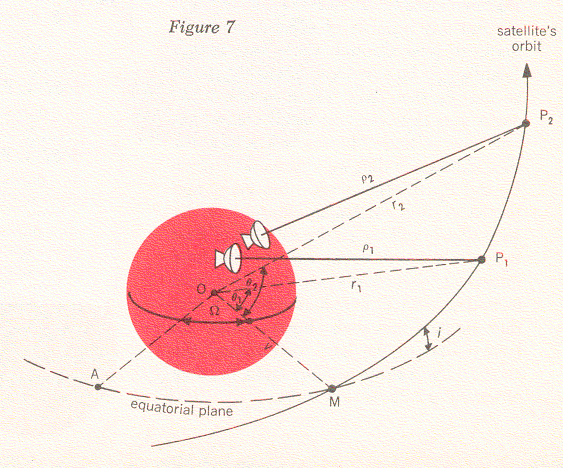
However, we still do not know the length and the width of the particular ellipse the satellite is following and how this orbit is oriented within the orbital plane. Let us imagine again that we can stand off to one side of the orbit and take a good look at it; Figure 8 shows us what we would see. There are the two points P₂ and P₁ at which we have observed the satellite. We know the positions of these points relative to each other and in relation to the center of the earth, because we have already calculatred r₂, r₁, θ₂ and θ₁, but any number of ellipses could be made to pass through these two points. Some might be very large, others might be so narrow that they would intersect the earth and thus be impossible. However, only one of these ellipses will satisfy the time difference that we observed between P₁ and P₂. In other words, the shape and period of this particular ellipse must be such that it will cause the satellite to pass through P₁ and P₂ in exactly the time interval t₂ - t₁. If we work out our time formulas, we will convince ourselves that there is only one such ellipse. When we have found it, we have determined the orbit of the Telstar satellite from the two observed positions and times.

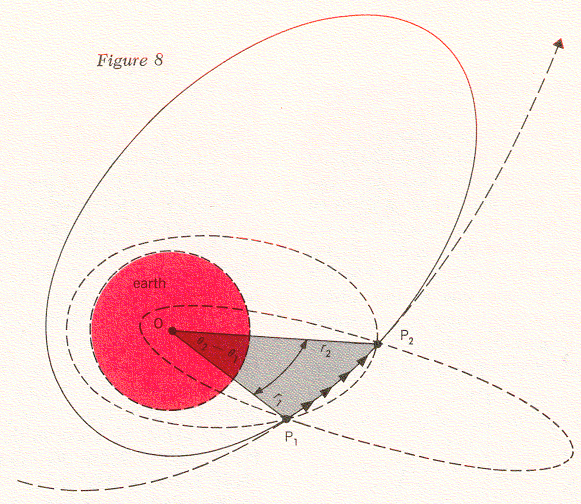
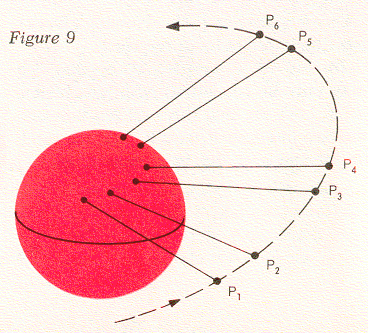
In principle then, we could keep track of the Telstar satellite by making a pair of observations P₁ and P₂, and then predicting ahead a short segment of an orbit that is the ellipse we have computed. After a while we must verify this ellipse with two more observations P₃ and P₄, predict ahead over another segment, and verify again with P₅ and P₆ (see Figure 9). The reason we have to keep taking new measurements is that the elliptic orbit does not remain the same. As we discussed in connection with Echo I, the orbital plane will "wobble" about the earth because of the equatorial bulge. We also know that the orbit's major axis will revolve within the orbital plane. As we have seen before, these effects are small and can be represented by appropriate mathematical formulas. If we calculate them, we will see the connection between one pair of observations and a later one, and eventually we can increase the time interval between successive pairs of observations. There are also mathematical formulas that we can use to predict the position of the satellite for many revolutions in its elliptic orbit.

In order to predict orbits successfully, we must also realize that the measurements we obtain from a precision tracker, such as the angles A and E and the distance ρ, are always subject to small inaccuracies. Thus it is not really possible to take just two measurements like P₁ and P₂ and determine a satisfactory orbit from them. In reality, our tracker takes many readings, and these are averaged to give adequate information about the orbit. Therefore, the picture we have in mind is not quite like Figure 7, but rather like Figure 10. Here the trackers have established a series of points that are somewhat scattered, and by taking averages we can calculate an orbit that passes through them in a smooth fashion.

The trackers we have mentioned so far have given us azimuth and elevation angles and also the distance to the satellite at every instant. Sometimes we must use simpler instruments that do not yield all this information. They might, for instance, only give us the two angles. The mathematics of calculating an orbit from such measurements is somewhat different, but the process is fundamentally the same as we have discussed here.

When you do these calculations for the Telstar satellite from one day to the next - and especially if you have more than one satellite to keep track of - the amount of work will become quite large. Nowadays our calculations are done for us on electronic computers, which both receive information from the tracking instruments automatically through Teletype or DataPhone channels and send back information concerning future positions of the satellite to the ground stations. There are still quite a few problems to be solved, and we are presently working on ways of making all this equipment perform the orbit predictions for the Telstar satellites automatically and efficiently.

Franz T. Geyling was born in Tientsin, China, and received a B.S. in 1950, an M.S. in 1951, and a Ph.D. in 1954 from Stanford University. He joined Bell Telephone Laboratories in 1954, and has been engaged in celestial mechanics studies of rockets and satellites, as well as stress analysis of submarine cables.